Visualizing Expectation Maximization

k-means vs. Gaussian Mixture Models (GMM)

Author

Connor Robertson

Overview

I recently read a great overview of Gaussian Mixture Models and thought, “Man, I’d like to see this clustering visualized.” So here I am to visualize it myself.

Expectation maximization (EM)

Best thing to do is just read the Wikipedia, but the general procedure here is:

Important 1: EM steps
  1. Sample some points from a distribution
  2. Find the expected value of each point
  3. Adjust parameters to maximize the expected values of the points
  4. Repeat 2 and 3

That’s all very abstract, but I will define it for each of our cases more concretely (which, fortunately, are simple).

k-means

k-means is a clustering algorithm that looks to find \(k\) clusters in a dataset which are parametrized by the mean of the cluster. Go figure. The naive algorithm for k-means is Lloyd’s algorithm which has the following steps (in a similar spirit to EM):

Important 2: k-means steps
  1. Sample \(k\) reasonable cluster centers from your domain
  2. Compute the closest of the \(k\) centers for each of your data points
  3. Adjust the locations of the \(k\) centers to be the center of the corresponding data points
  4. Repeat 2 and 3

Creating sample data

To explore this idea, let’s consider two sets of sample data from some Gaussian distributions in two dimensions. The first will be circular (diagonal covariance matrix) and the second will be skewed (dense covariance matrix). Let’s write this out in simple code:

Imports 
using Distributions
using Random
using LinearAlgebra
using StatsBase
using CairoMakie
using Colors
using ColorSchemes
cmap = ColorSchemes.seaborn_colorblind6;
Distribution creation functions 
function create_spherical_gaussian(mu, var)
    cov = diagm(ones(length(mu)) .* var)
    return MvNormal(mu, cov)
end

function create_oblong_gaussian(mu, cov)
    return MvNormal(mu, cov)
end;
# Settings
n_distributions = 5
n_samples = 20

# Means/variances/covariances
Random.seed!(1234)
means = [2i*rand(2) for i in 1:n_distributions]
vars_1 = [0.2*i*rand() for i in 1:n_distributions]
covs_2 = []
for i in 1:n_distributions
    cov = 0.2i*rand(2,2)
    cov = cov' * cov # Ensure its positive definite
    push!(covs_2, cov)
end

# Create distributions
dists_1 = [create_spherical_gaussian(m, v) for (m,v) in zip(means, vars_1)]
dists_2 = [create_oblong_gaussian(m, c) for (m,c) in zip(means, covs_2)]

# Sample distributions
samples_1 = [rand(d, n_samples) for d in dists_1]
samples_2 = [rand(d, n_samples) for d in dists_2]

# Create datasets (combine samples and shuffle)
data_1 = hcat(samples_1...)[:,randperm(n_distributions*n_samples)]
data_2 = hcat(samples_2...)[:,randperm(n_distributions*n_samples)];

We can plot the samples we’ve taken from the distributions to get a sense of the clustering:

fig = Figure(size=(800,400))
ax1 = Axis(fig[1,1])
ax2 = Axis(fig[1,2])
for i in 1:n_distributions
    scatter!(ax1, samples_1[i][1,:], samples_1[i][2,:], color=cmap[i], label=nothing)
    scatter!(ax2, samples_2[i][1,:], samples_2[i][2,:], color=cmap[i], label="Distribution $i")
end
hidedecorations!(ax1, ticklabels=false)
hidedecorations!(ax2, ticklabels=false)
axislegend(ax2; position=:lt)
display(fig);
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220

Implementation

Now that we have some sample data to try to cluster, let’s implement a simple k-means algorithm using the steps in Important 2:

Utilities 
function distances_to_center(data, center)
    distances = zeros(size(data,2))
    for i in 1:size(data,2)
        distances[i] = mean((data[:,i] .- center).^2)
    end
    return distances
end

function plot_cluster_results!(fig, centers, labels, data, true_data)
    n_clusters = length(true_data)
    k = size(centers, 2)

    ax1 = Axis(fig[1,1])
    ax2 = Axis(fig[1,2])
    for i in 1:k
        approx_cluster = data[:,labels .== i]
        scatter!(ax1, approx_cluster[1,:], approx_cluster[2,:], color=cmap[i], label="Approx cluster $i")
        scatter!(ax1, [centers[1,i]], [centers[2,i]], color=cmap[i], marker=:star5, markersize=10, label=nothing, strokewidth=2)
    end
    for i in 1:n_clusters
        scatter!(ax2, true_data[i][1,:], true_data[i][2,:], color=cmap[i], label="True cluster $i")
    end
    hidedecorations!(ax1, ticklabels=false)
    hidedecorations!(ax2, ticklabels=false)
    axislegend(ax1; position=:rb)
    axislegend(ax2; position=:rb)
    return fig
end;

function animate_kmeans!!(centers, data_labels, data, samples, filename)
    fig = Figure(size=(800,400))
    record(fig, filename; framerate=2) do io
        converged = false
        nsteps = 1
        while converged == false
            # Clear the figure
            empty!(fig)

            # Step
            converged = kmeans!!(centers, data_labels, data, 1)

            # Plot
            plot_cluster_results!(fig, centers, data_labels, data, samples)
            text!(fig.scene, 5, 0, text="Step: $nsteps", font=:bold)

            # Capture frame
            recordframe!(io)
            nsteps += 1
        end
    end
end;
kmeans 
function kmeans!!(centers, data_labels, data, max_steps=100, tol=1e-5)
    k = size(centers,2)
    center_shift = Inf * ones(k)
    nsteps = 0

    while (maximum(center_shift) > tol) & (nsteps < max_steps)
        # Compute the distance from each center to our data and assign closest
        distances = hcat([distances_to_center(data, c) for c in eachcol(centers)]...)
        data_labels .= [argmin(d) for d in eachrow(distances)]

        # Reassign centers to mean of closest data
        for i in 1:k
            closest_data = data[:,data_labels .== i]
            new_center = mean(closest_data, dims=2)
            center_shift[i] = norm(centers[:,i] .- new_center)
            centers[:,i] .= new_center
        end
        nsteps += 1
    end
    return (maximum(center_shift) < tol)
end
kmeans!! (generic function with 3 methods)
# Sample initial cluster centers within our sample data
Random.seed!(1)
k = 5
smin = minimum(data_1, dims=2)
smax = maximum(data_1, dims=2)
centers = (smax - smin) .* rand(2,k) .+ smin
data_labels = ones(Int64, size(data_1,2))

# Repeat steps 2 and 3 until centers aren't moving
kmeans!!(centers, data_labels, data_1)

# Visualize results
fig = Figure(size=(800,400))
plot_cluster_results!(fig, centers, data_labels, data_1, samples_1)
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220

Notice that the results are highly dependent on our initial sampling. If we adjust the random seeding for the initial centers, we don’t get such nice results:

# Sample initial cluster centers within our sample data
Random.seed!(2)
k = 5
smin = minimum(data_1, dims=2)
smax = maximum(data_1, dims=2)
centers = (smax - smin) .* rand(2,k) .+ smin
data_labels = ones(size(data_1,2))

# Execute
kmeans!!(centers, data_labels, data_1)

# Visualize results
fig = Figure(size=(800,400))
plot_cluster_results!(fig, centers, data_labels, data_1, samples_1)
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220

We can also try this on our second dataset:

# Sample initial cluster centers within our sample data
Random.seed!(1)
k = 5
smin = minimum(data_2, dims=2)
smax = maximum(data_2, dims=2)
centers = (smax - smin) .* rand(2,k) .+ smin
data_labels = ones(size(data_2,2))

# Execute
kmeans!!(centers, data_labels, data_2)

# Visualize results
fig = Figure(size=(800,400))
plot_cluster_results!(fig, centers, data_labels, data_2, samples_2)
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220

Animating the process

Now, the entire purpose of this document is actually to visually explore the methods as they evolve, so let’s set up some animation structure. Fortunately, Makie.jl makes this easy. We only need to iteratively take a step and capture the plotted frame at each step.

Random.seed!(5)
k = 5
smin = minimum(data_1, dims=2)
smax = maximum(data_1, dims=2)
centers = (smax - smin) .* rand(2,k) .+ smin
data_labels = ones(size(data_1,2))

animate_kmeans!!(centers, data_labels, data_1, samples_1, "gifs/kmeans.gif")
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220
"gifs/kmeans.gif"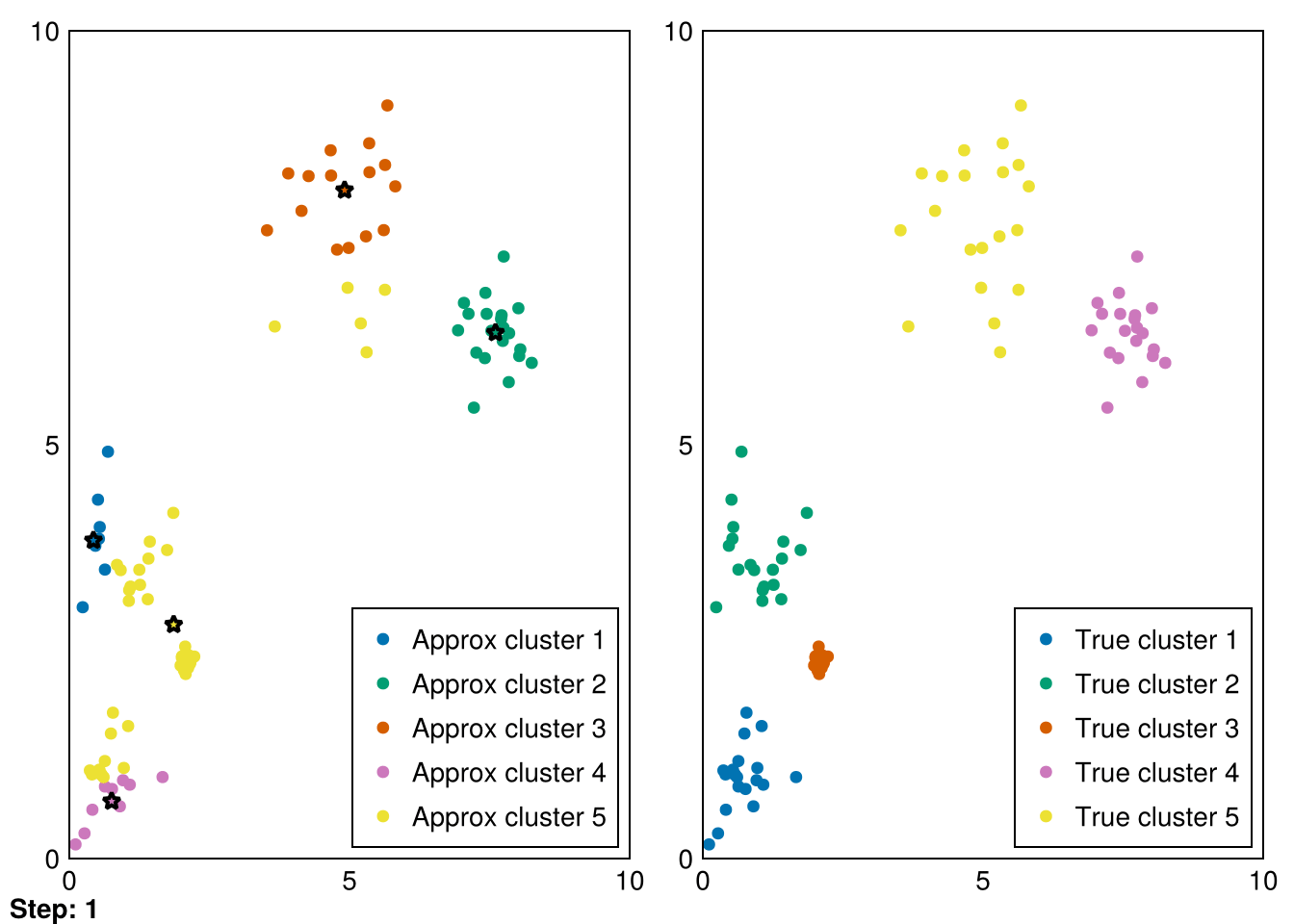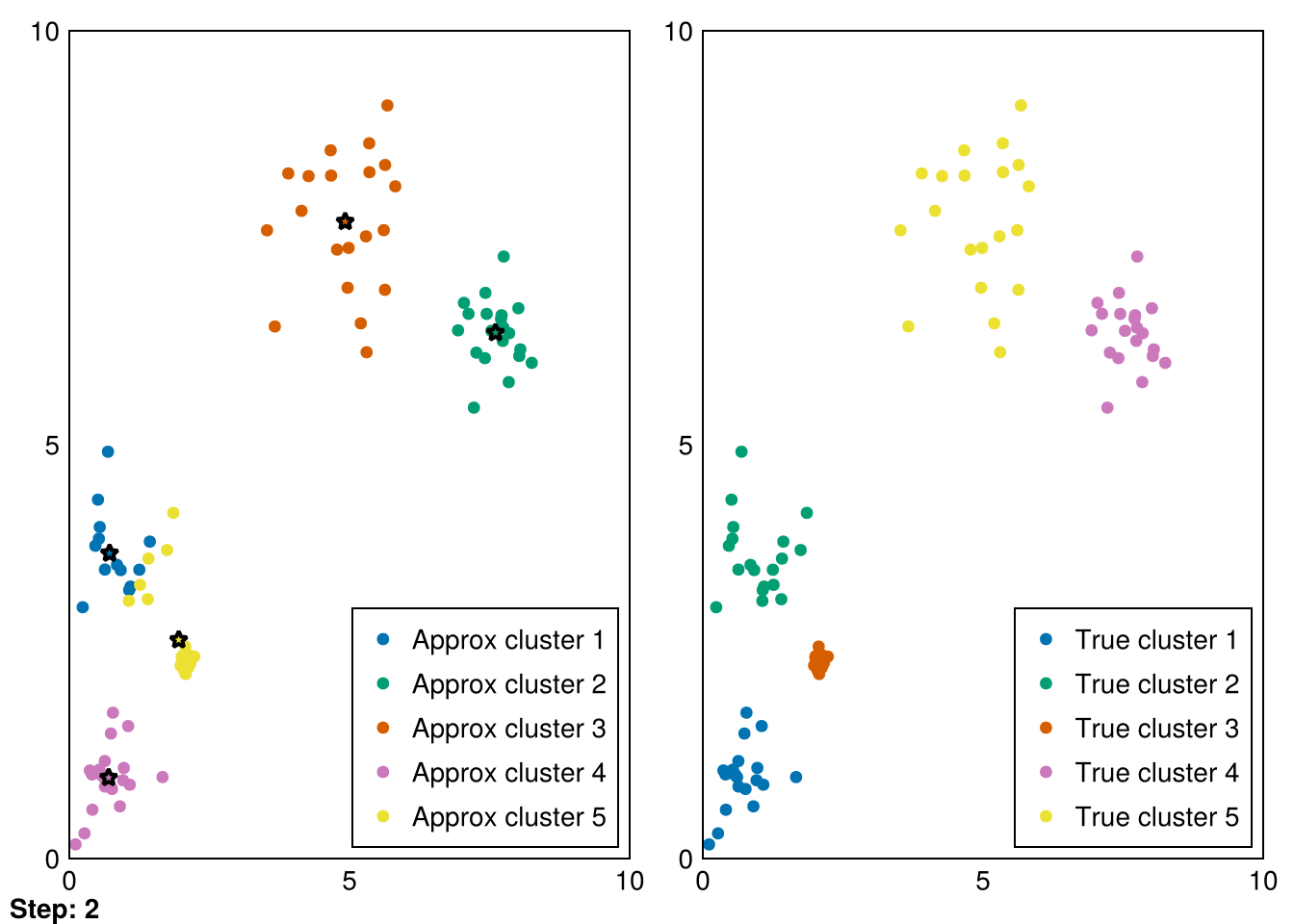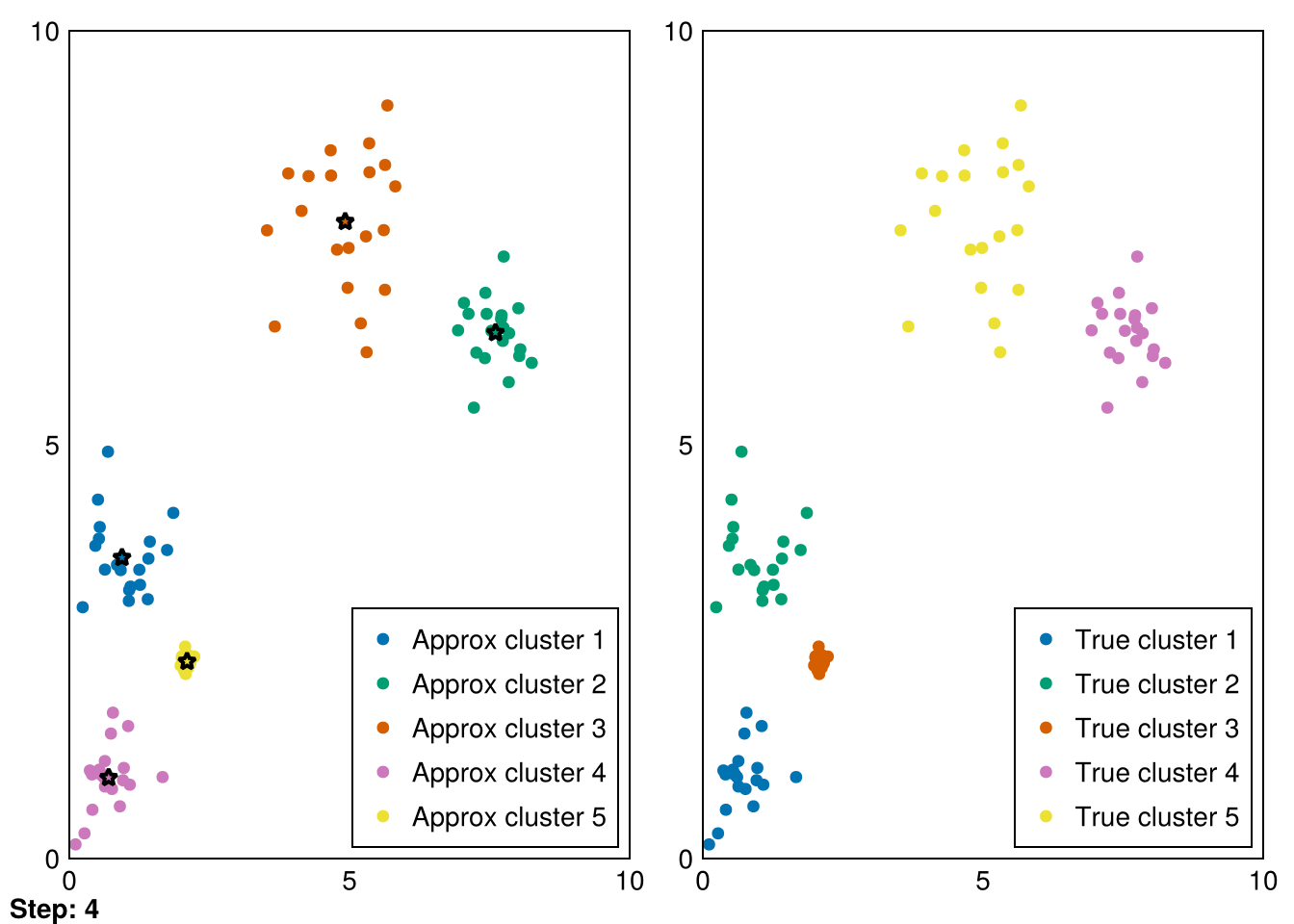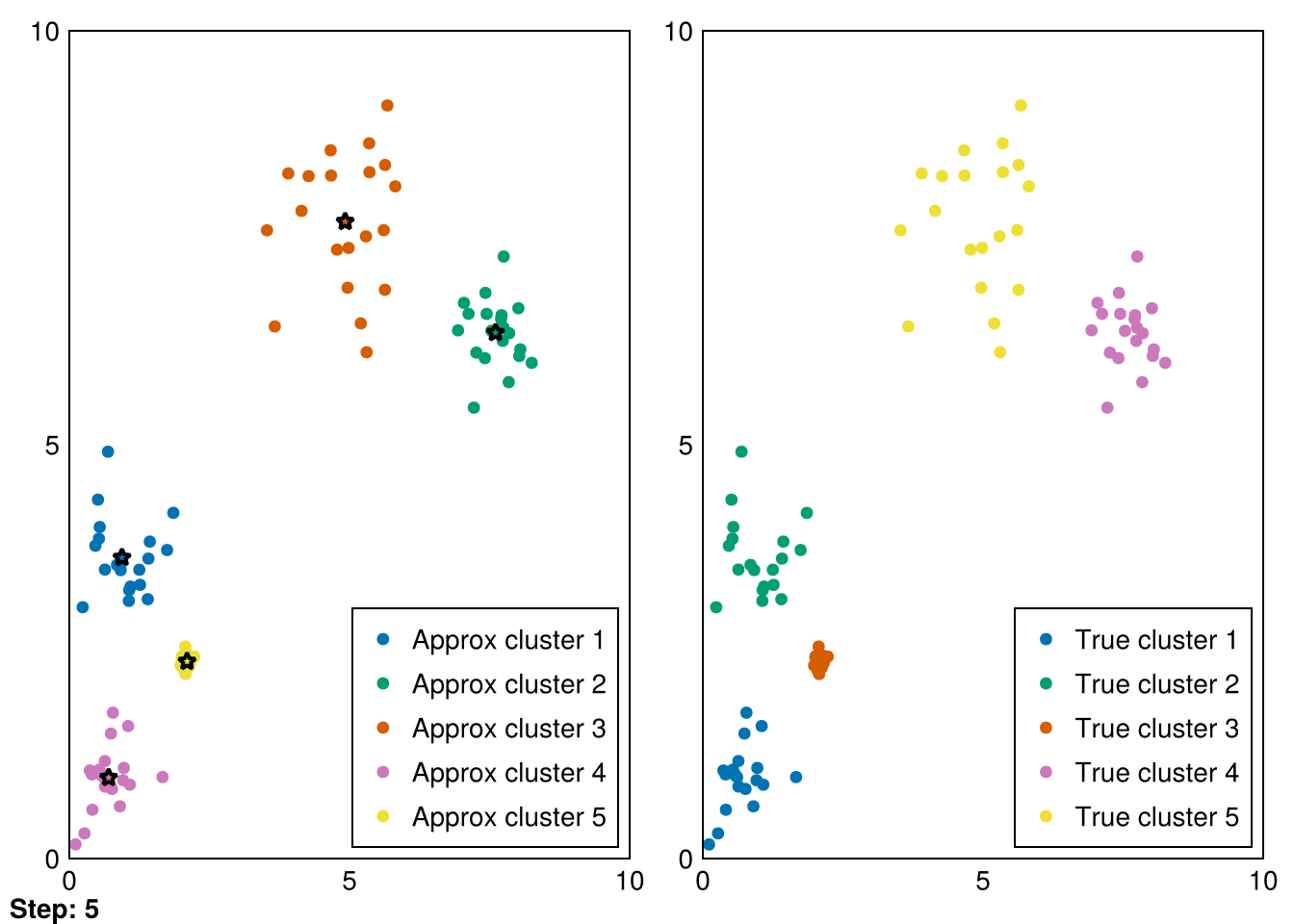

Amazing! Now we can see the progress of kmeans in each step (where the stars represent the cluster means).

Gaussian Mixture Models (GMM)

Gaussian mixture models really boil down to using a Gaussian distribution for each cluster. With these cluster distributions, we can assign a cluster probability to each data point and then subsequently update the distributions to new means and covariances. This procedure is a true EM process because it aims to maximize the probability of cluster inclusion for each datapoint.

The naive algorithm for this EM procedure is as follows:

Important 3: GMM steps
  1. Sample \(k\) reasonable cluster means and covariances for Gaussians from your domain
  2. Compute the PDF values corresponding to each Gaussian and normalize to get cluster probabilities for each datapoint
  3. Adjust the means and covariances of the \(k\) Gaussians using the cluster probabilities from each datapoint
  4. Repeat 2 and 3

Implementing EM

To start, we are going to implement Important 3 by considering spherical Gaussians in which the covariance is a diagonally constrained.

Utilities 
function plot_gaussians(gaussians)
# Show initial gaussian clusters
    fig = Figure()
    ax = Axis(fig[1,1])
    sample_x = range(smin[1], smax[1], 1000)
    sample_y = range(smin[2], smax[2], 1000)
    for (i,g) in enumerate(gaussians)
        sample_pdfs = [pdf(g, [x,y]) for x in sample_x, y in sample_y]
        sample_pdfs ./= sum(sample_pdfs)
        my_colormap = reverse([cmap[i]*(1 - j/256) + RGB(1, 1, 1)*(j/256) - RGBAf(0,0,0,j/256) for j in 0:256-1])
        contourf!(sample_x, sample_y, sample_pdfs, colormap=my_colormap, label="Gaussian $i")
    end
    axislegend(ax; position=:rb)
    hidedecorations!(ax, ticklabels=false)
end

function plot_gmm_results!(fig, gaussians, labels, data, true_data)
    n_clusters = length(true_data)
    k = size(centers, 2)

    sample_x = range(smin[1], smax[1], 1000)
    sample_y = range(smin[2], smax[2], 1000)
    ax1 = Axis(fig[1,1])
    ax2 = Axis(fig[1,2])
    for i in 1:k
        approx_cluster = data[:,labels .== i]
        scatter!(ax1, approx_cluster[1,:], approx_cluster[2,:], color=cmap[i], label="Approx cluster $i")
        sample_pdfs = [pdf(gaussians[i], [x,y]) for x in sample_x, y in sample_y]
        my_colormap = reverse([cmap[i]*(1 - j/256) + RGB(1, 1, 1)*(j/256) - RGBAf(0,0,0,j/256) for j in 0:256-1])
        contourf!(ax1, sample_x, sample_y, sample_pdfs, colormap=my_colormap, label=nothing)
    end
    for i in 1:n_clusters
        scatter!(ax2, true_data[i][1,:], true_data[i][2,:], color=cmap[i], label="True cluster $i")
    end
    hidedecorations!(ax1, ticklabels=false)
    hidedecorations!(ax2, ticklabels=false)
    axislegend(ax1; position=:rb)
    axislegend(ax2; position=:rb)
    return fig
end;

# Execute one step at a time, visualize results at each step, then record a frame
function animate_gmm!!(gaussians, data_labels, data, samples, filename)
    fig = Figure(size=(800,400))
    record(fig, filename; framerate=2) do io
        converged = false
        nsteps = 1
        while converged == false
            # Clear the figure
            empty!(fig)

            # Step
            converged = gmm!!(gaussians, data_labels, data, 1)

            # Plot
            plot_gmm_results!(fig, gaussians, data_labels, data, samples)
            text!(fig.scene, 5, 0, text="Step: $nsteps", font=:bold)

            # Capture frame
            recordframe!(io)
            nsteps += 1
        end
    end;
end
animate_gmm!! (generic function with 1 method)
# Sample initial cluster means and variances
Random.seed!(1)
k = 5
smin = minimum(data_1, dims=2)
smax = maximum(data_1, dims=2)
means = (smax - smin) .* rand(2,k) .+ smin
vars = ones(k)
gaussians = [MvNormal(means[:,i],vars[i]) for i in 1:k]
data_labels = ones(Int64, size(data_1,2))

plot_gaussians(gaussians);
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220

As you can observe, we have some great circular starting distributions. We now need to align these with the data. Let’s implement the GMM procedure from Important 3:

GMM 
function gmm!!(gaussians::Vector{IsoNormal}, data_labels, data, max_steps=100, tol=1e-5)
    k = length(gaussians)
    ll_shift = 10.0
    nsteps = 0
    gweights = ones(k) ./ k
    data_weights = zeros(length(data_labels),k)

    while (ll_shift > tol) & (nsteps < max_steps)
        # Compute the pdfs for each datapoint to each gaussian and assign the most probable
        cluster_probs = hcat([pdf(g, data) for g in gaussians]...)
        ll_old = sum(log.(cluster_probs * gweights))
        all_weight = cluster_probs * gweights
        data_weights .= gweights' .* cluster_probs ./ all_weight

        # Reassign gaussians to weighted means and std devs
        for i in 1:k
            Nk = sum(data_weights[:,i])
            new_mean = sum(data .* data_weights[:,i]', dims=2) ./ Nk
            new_std = sqrt(mean(sum((data .- new_mean).^2 .* data_weights[:,i]', dims=2) ./ Nk))
            gaussians[i] = MvNormal(vec(new_mean), new_std)
        end

        # Check change in log likelihood for convergence
        cluster_probs = hcat([pdf(g, data) for g in gaussians]...)
        ll_new = sum(log.(cluster_probs * gweights))
        ll_shift = ll_new - ll_old
        ll_old = ll_new
        nsteps += 1
    end
    data_labels .= [argmax(d) for d in eachrow(data_weights)]
    return (ll_shift < tol)
end;

Now, let’s put it all together and run it for our initial distributions.

Random.seed!(5)
k = 5
smin = minimum(data_1, dims=2)
smax = maximum(data_1, dims=2)
means = (smax - smin) .* rand(2,k) .+ smin
vars = ones(k)
gaussians = [MvNormal(means[:,i],vars[i]) for i in 1:k]
data_labels = ones(Int64, size(data_1,2))

animate_gmm!!(gaussians, data_labels, data_1, samples_1, "gifs/gmm1.gif");
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220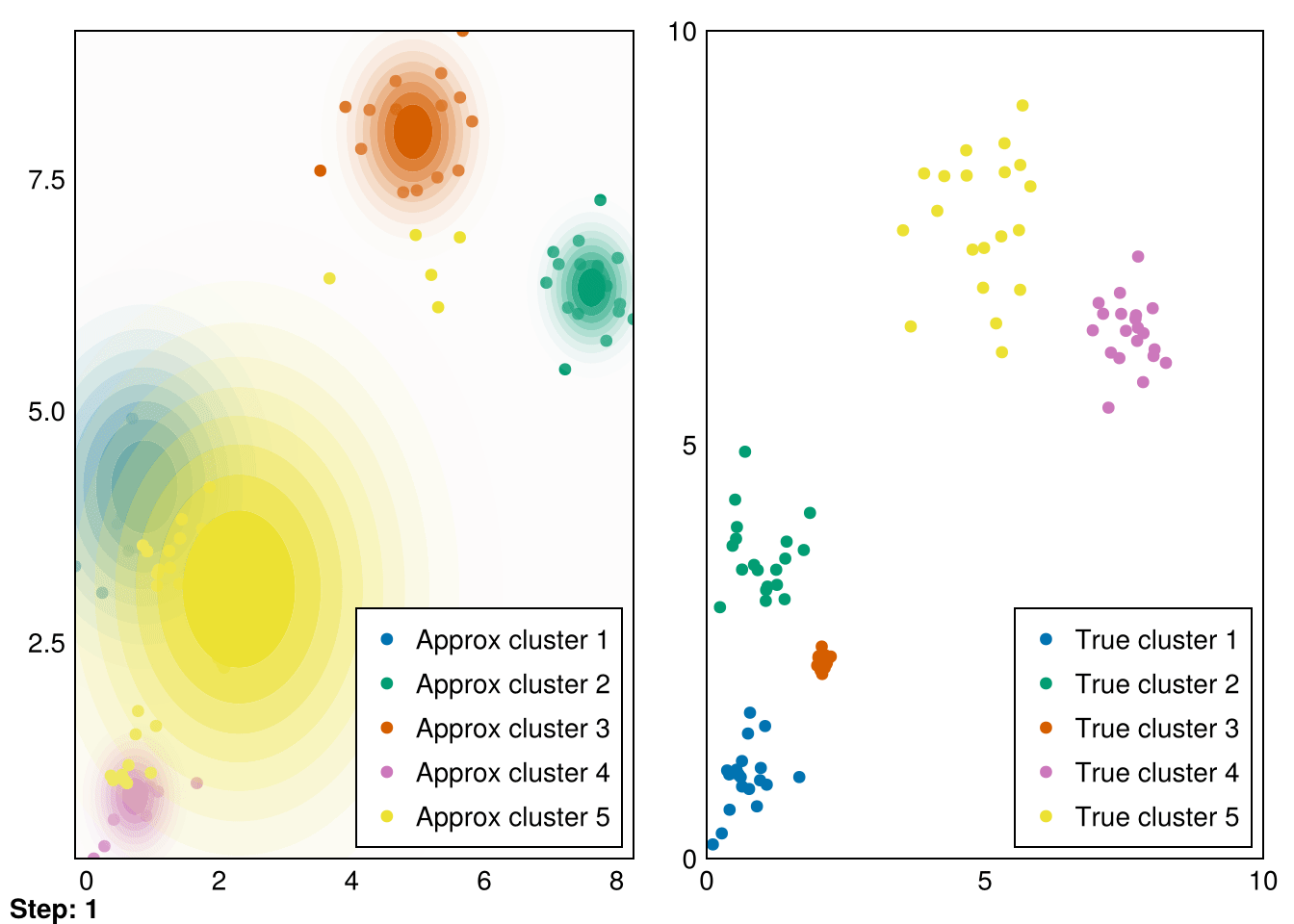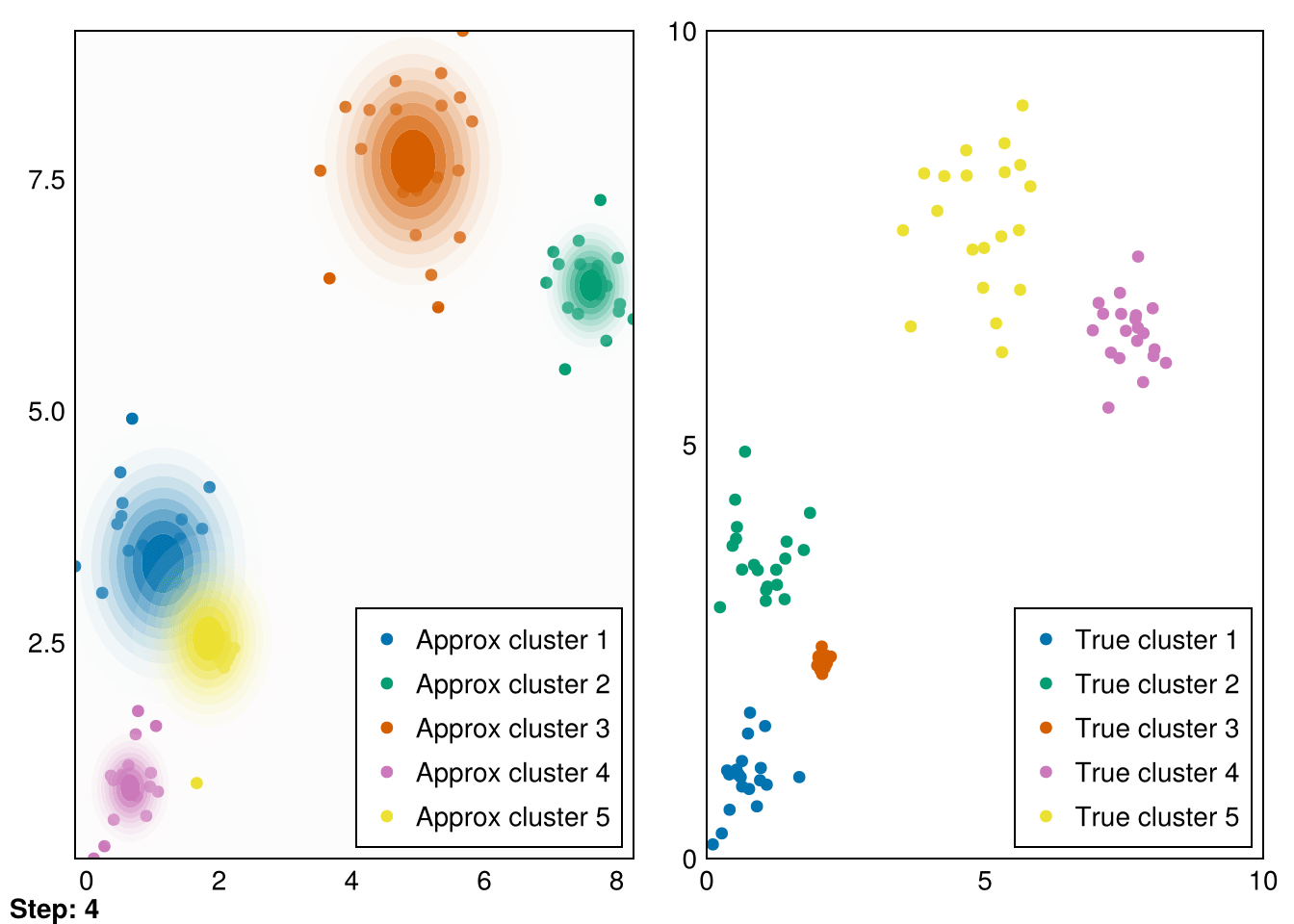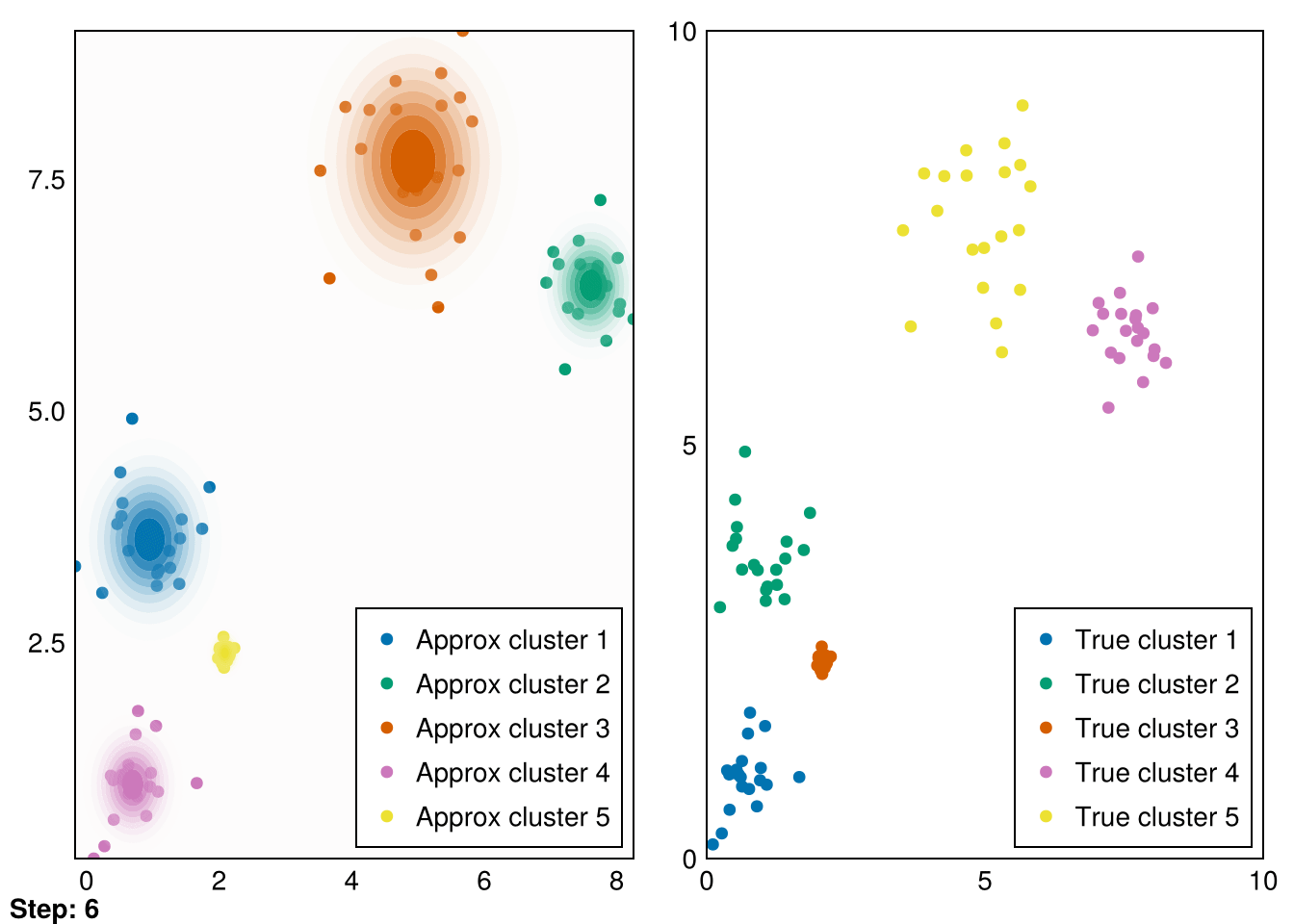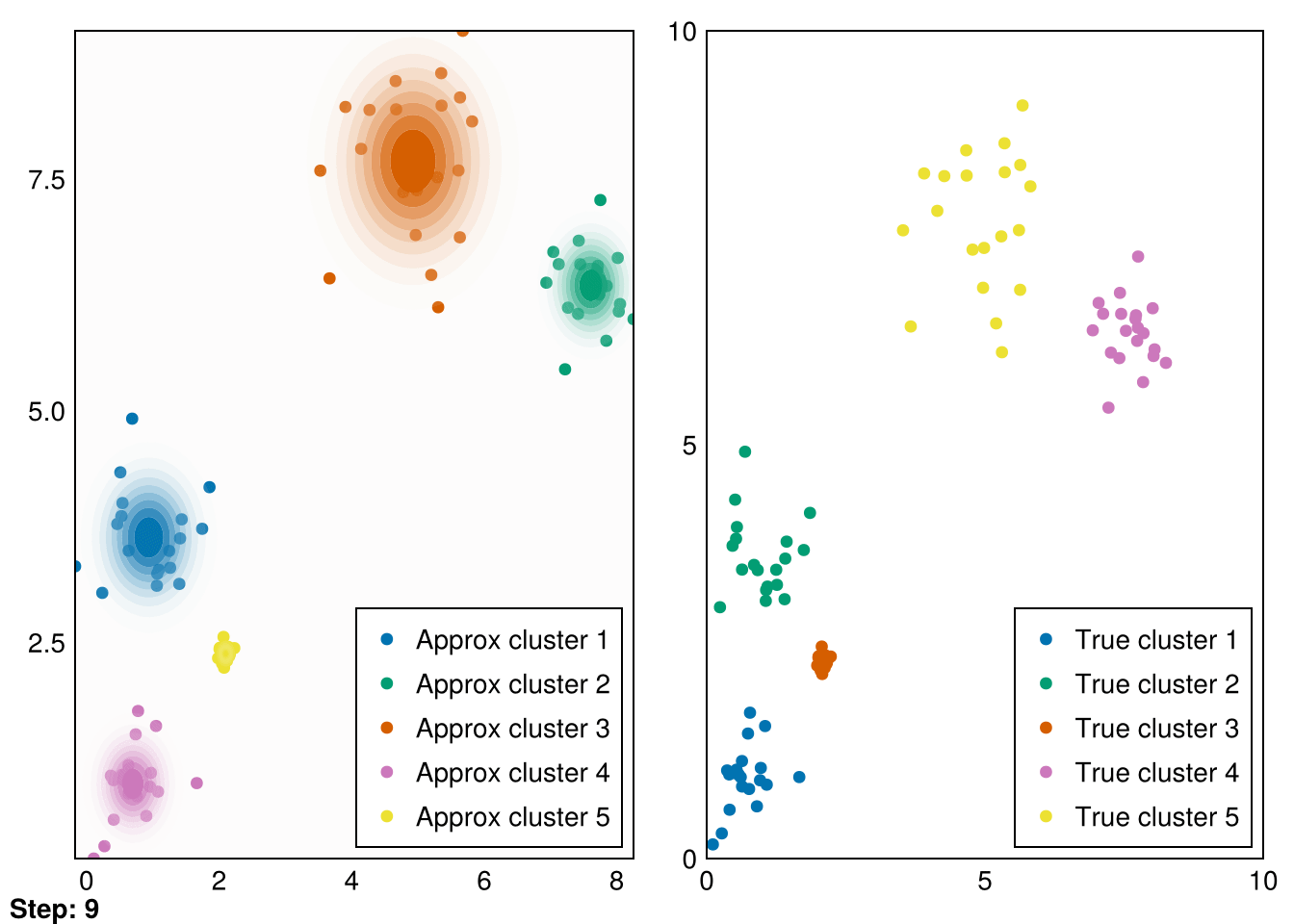

Great! These are pretty good fits. However, applying it to our second dataset quickly reveals that spherical Gaussians just won’t cut it:

Random.seed!(1)
k = 5
smin = minimum(data_1, dims=2)
smax = maximum(data_1, dims=2)
means = (smax - smin) .* rand(2,k) .+ smin
vars = ones(k)
gaussians = [MvNormal(means[:,i],vars[i]) for i in 1:k]
data_labels = ones(Int64, size(data_2,2))

animate_gmm!!(gaussians, data_labels, data_2, samples_2, "gifs/gmm2.gif");
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220

Instead, we can modify our calculation of the variance in the gmm!! function to calculate the full covariance matrix:

GMM (full covariance) 
function gmm!!(gaussians::Vector{FullNormal}, data_labels, data, max_steps=100, tol=1e-5)
    k = length(gaussians)
    ll_shift = 10.0
    nsteps = 0
    gweights = ones(k) ./ k
    data_weights = zeros(length(data_labels),k)

    while (ll_shift > tol) & (nsteps < max_steps)
        # Compute the pdfs for each datapoint to each gaussian and assign the most probable
        cluster_probs = hcat([pdf(g, data) for g in gaussians]...)
        ll_old = sum(log.(cluster_probs * gweights))
        all_weight = cluster_probs * gweights
        data_weights .= gweights' .* cluster_probs ./ all_weight

        # Reassign gaussians to weighted means and std devs
        for i in 1:k
            Nk = sum(data_weights[:,i])
            new_mean = sum(data .* data_weights[:,i]', dims=2) ./ Nk
            new_std = mean([(d .- new_mean)*(d .- new_mean)' for d in eachcol(data)], weights(data_weights[:,i]))
            gaussians[i] = MvNormal(vec(new_mean), new_std)
        end

        # Check change in log likelihood for convergence
        cluster_probs = hcat([pdf(g, data) for g in gaussians]...)
        ll_new = sum(log.(cluster_probs * gweights))
        ll_shift = ll_new - ll_old
        ll_old = ll_new
        nsteps += 1
    end
    data_labels .= [argmax(d) for d in eachrow(data_weights)]
    return (ll_shift < tol)
end;
Random.seed!(1)
k = 5
smin = minimum(data_1, dims=2)
smax = maximum(data_1, dims=2)
means = (smax - smin) .* rand(2,k) .+ smin
vars = []
for i in 1:k
    A = I(2) .+ rand(2,2)
    push!(vars,A' * A)
end
gaussians = [MvNormal(means[:,i],vars[i]) for i in 1:k]
data_labels = ones(Int64, size(data_2,2))

animate_gmm!!(gaussians, data_labels, data_2, samples_2, "gifs/gmm3.gif");
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220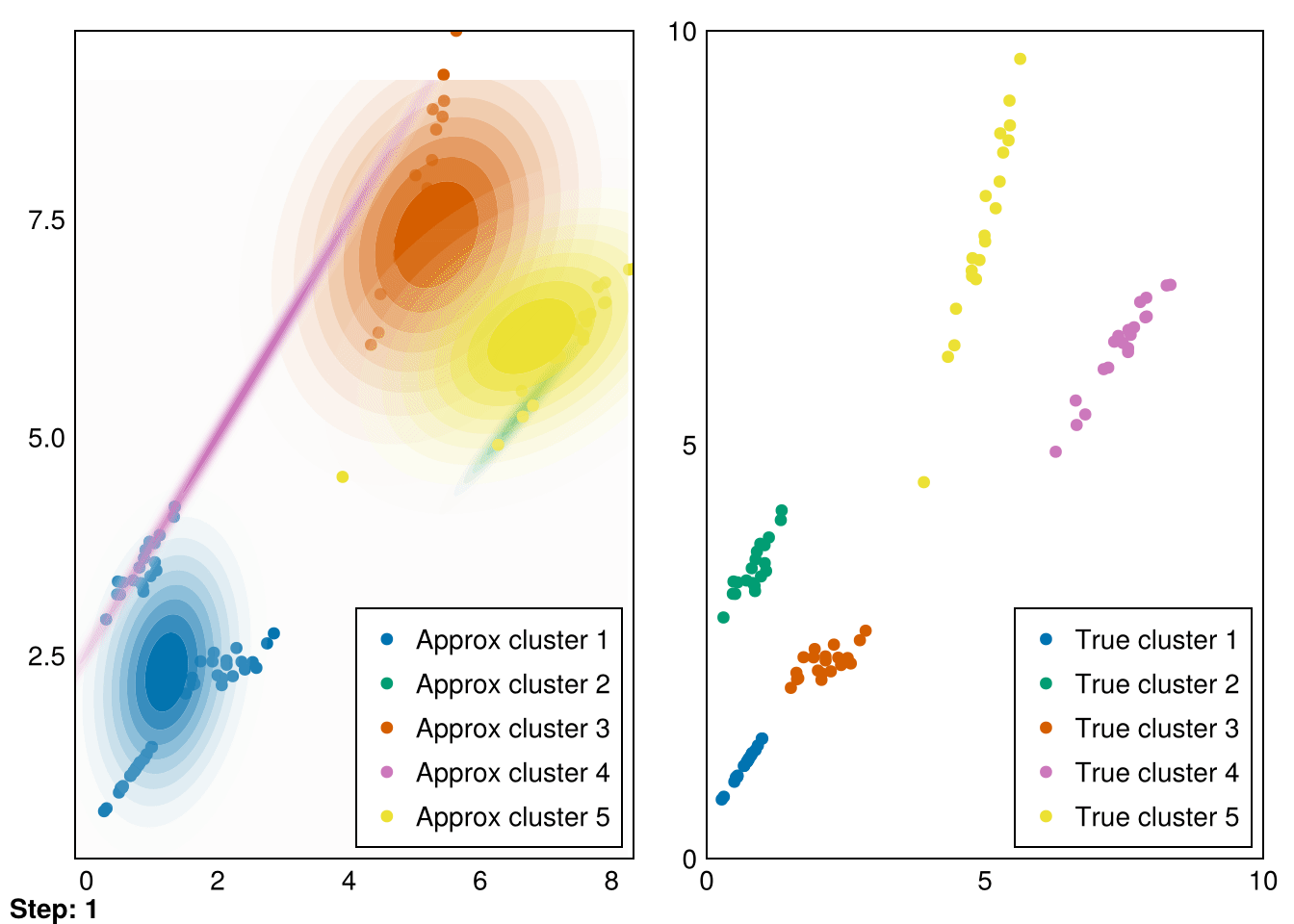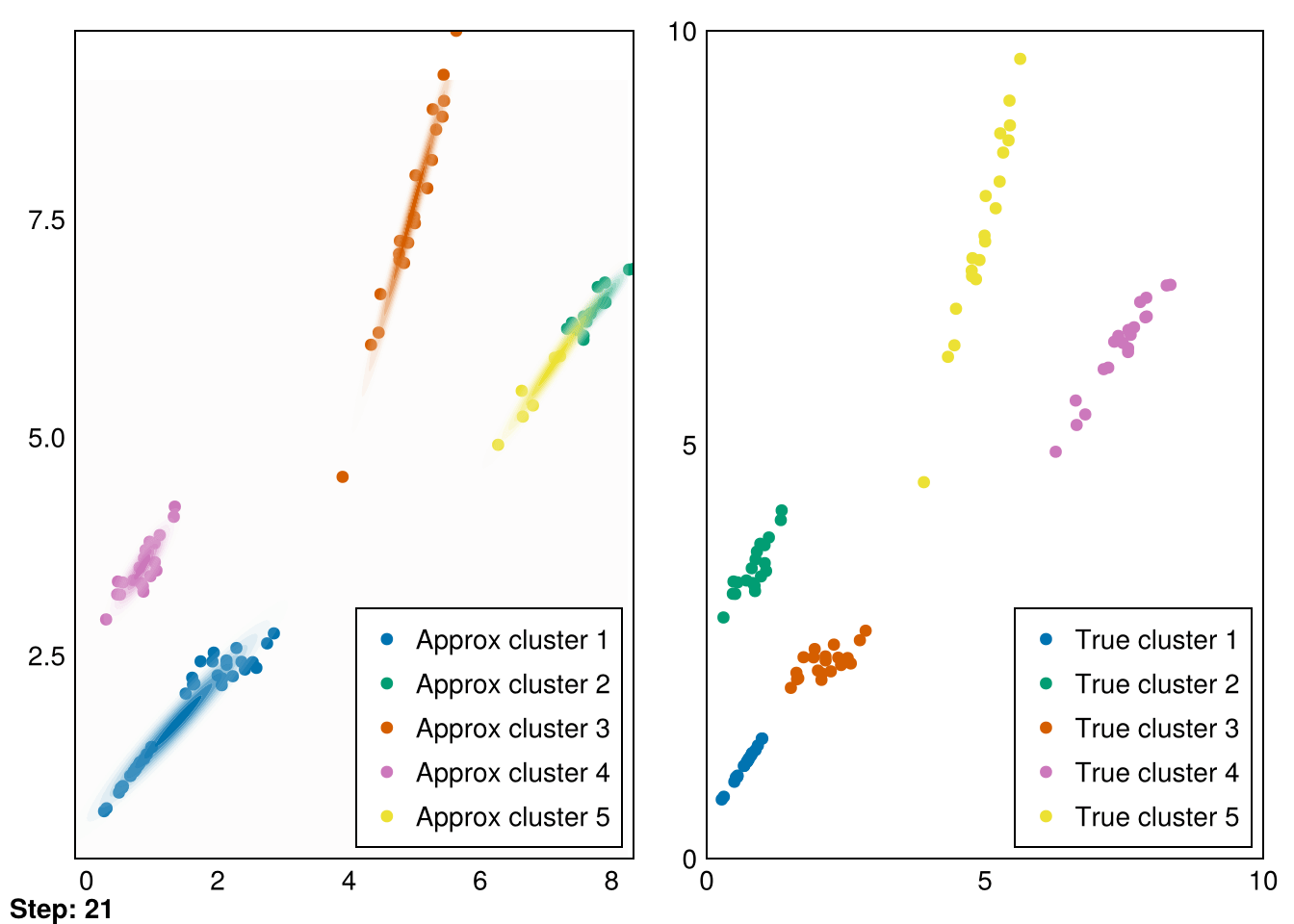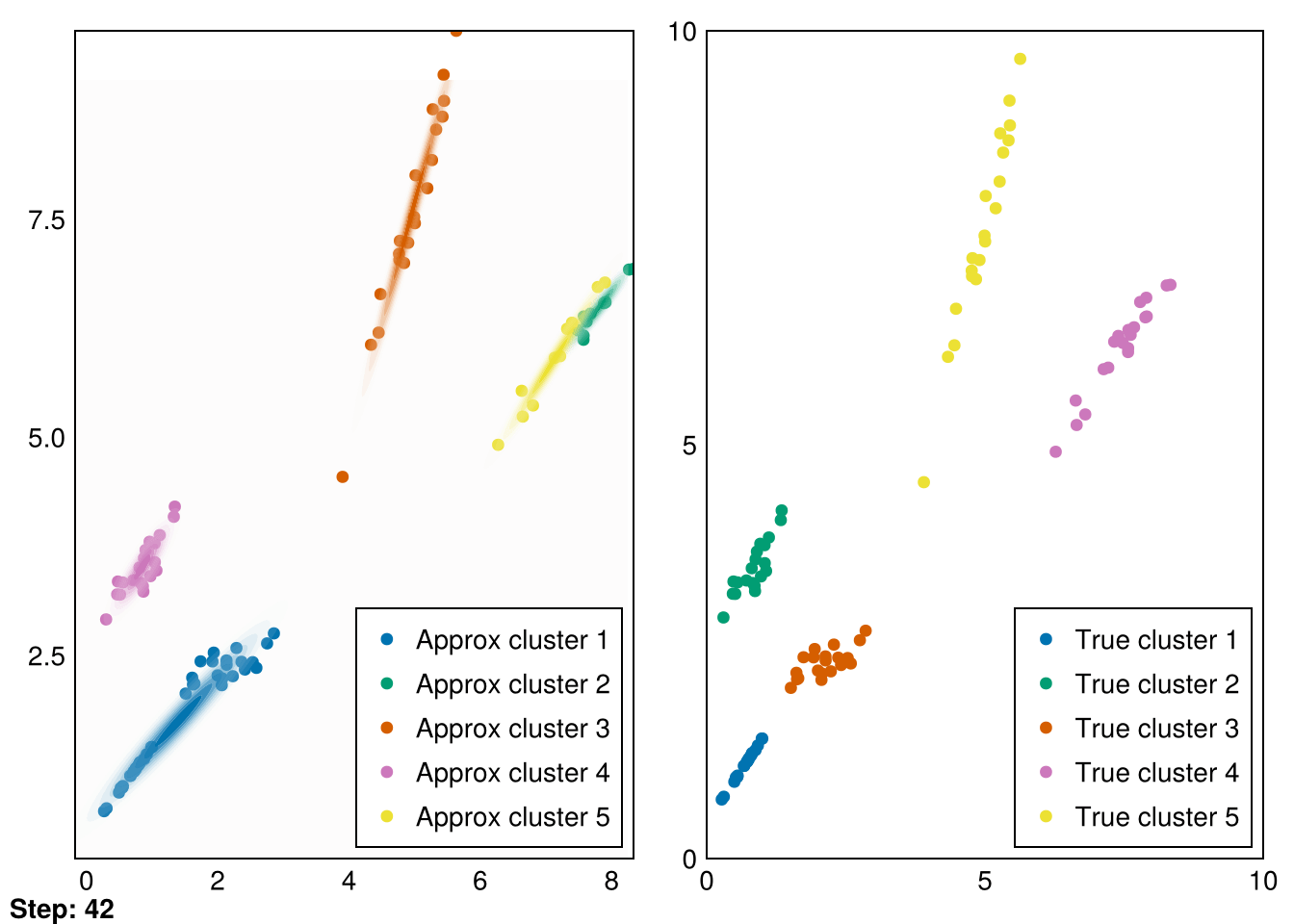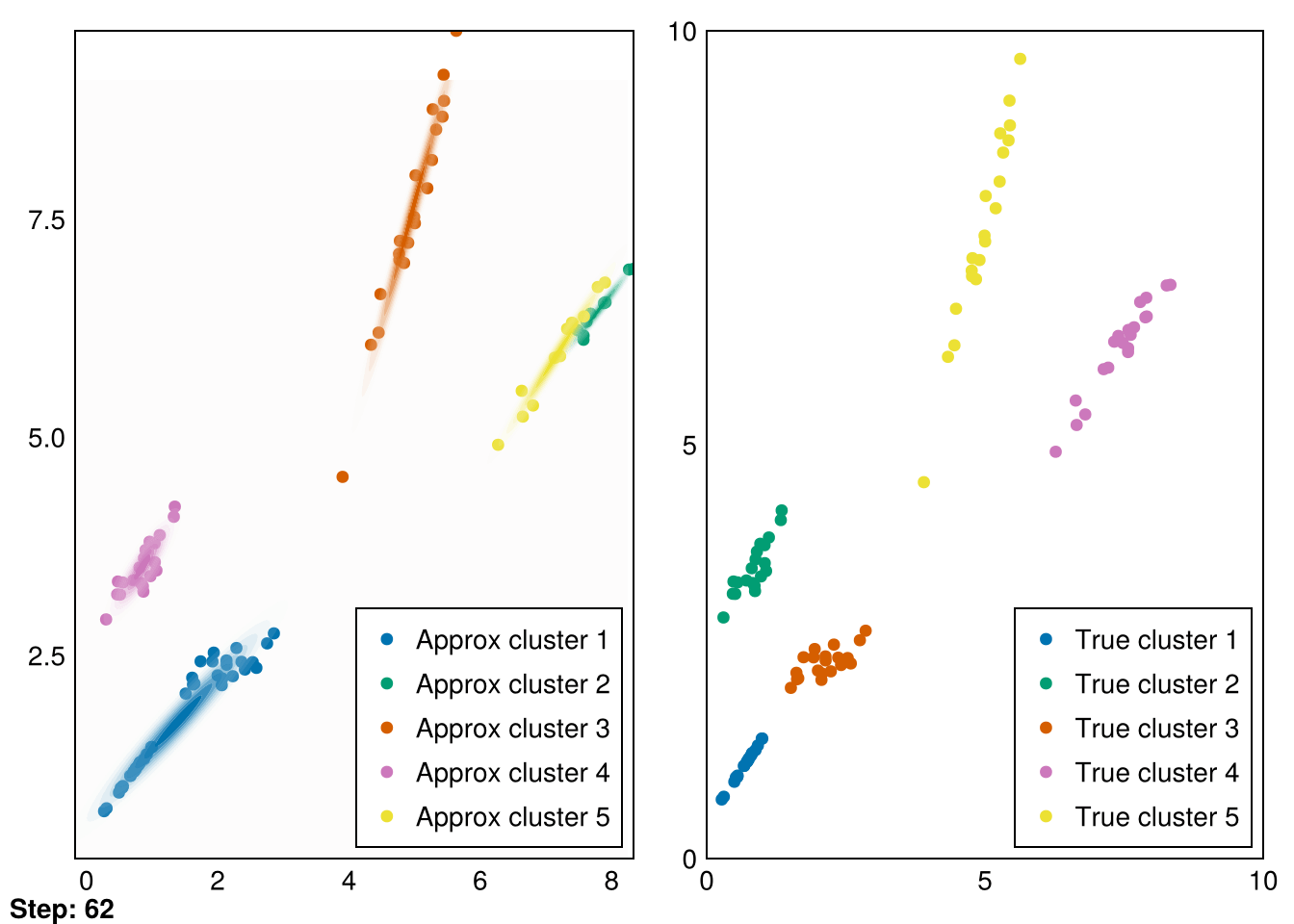

The clusters aren’t perfectly recovered (due to the initialization), but you can see that the Gaussians cover the data much more precisely.

Initializing clusters

Now that we have fully fledged approaches for clustering with expectation maximization, let’s consider better initializations:

  1. Forgy’s method: Sample \(k\) points from the data as starting centers
  2. Random partitions: Randomly assign cluster ids then average to yield the initial points
  3. kmeans++: Choose each mean from the data a large distance from the previously selected (proportional to the squared distance)
Plotting function 
function plot_centers!(fig, centers, true_data)
    n_clusters = length(true_data)
    k = size(centers, 2)

    ax1 = Axis(fig[1,1])
    for i in 1:n_clusters
        scatter!(ax1, true_data[i][1,:], true_data[i][2,:], color=cmap[i], label="True cluster $i")
    end
    for i in 1:k
        scatter!(ax1, [centers[1,i]], [centers[2,i]], color=:black, marker=:star5, markersize=10, label=nothing, strokewidth=2)
    end
    hidedecorations!(ax1, ticklabels=false)
    axislegend(ax1; position=:rb)
    return fig
end;
Initialization functions 
function forgy_init(data, k)
    return hcat(sample(eachcol(data), k, replace=false)...)
end
function random_init(data, k)
    cluster_ids = sample(1:k, size(data,2))
    return hcat([mean(data[:,cluster_ids .== i], dims=2) for i in 1:k]...)
end
function kpp_init(data, k)
    means = [sample(eachcol(data))]
    for i in 2:k
        dists = sum(hcat([norm.(eachcol(data .- m)).^2 for m in means]...), dims=2)
        dists ./= sum(dists)
        new_mean = sample(eachcol(data), weights(dists))
        push!(means, new_mean)
    end
    return hcat(means...)
end;
Random.seed!(1)
# Forgy
fig = Figure(size=(600,400))
centers = forgy_init(data_1, 5)
plot_centers!(fig, centers, samples_1)
fig.content[1].title = "Forgy"
display(fig);

# Random partition
fig = Figure(size=(600,400))
centers = random_init(data_1, 5)
plot_centers!(fig, centers, samples_1)
fig.content[1].title = "Random partition"
display(fig);

# Kpp
fig = Figure(size=(600,400))
centers = kpp_init(data_1, 5)
plot_centers!(fig, centers, samples_1)
fig.content[1].title = "Kpp";
display(fig);
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220

In this case, it is immediately obvious that the kmeans++ technique yielded the best, most spread centers that will work well with either our kmeans or GMM algorithms. On the other hand, the Forgy yielded data which was too clustered, something that can easily occur if there is an imbalance in representation between samples from different clusters. The Random partition approach gave points which were somewhat reasonable, but very centered. In this case, it is possible that kmeans or GMM does capture the correct cluster partitions, but also possible that some clusters are grouped.

Conclusion

Now, given improved initialization approaches, let’s rerun our kmeans and GMM approaches with random seeds that previously posed challenges:

Kmeans

# For dataset 1
Random.seed!(2)
k = 5
centers = kpp_init(data_1, k)
data_labels = ones(size(data_1,2))

kmeans!!(centers, data_labels, data_1)

fig = Figure(size=(800,400))
plot_cluster_results!(fig, centers, data_labels, data_1, samples_1)
display(fig);
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220

# For dataset 2
Random.seed!(2)
k = 5
centers = kpp_init(data_2, k)
data_labels = ones(size(data_2,2))

kmeans!!(centers, data_labels, data_2)

fig = Figure(size=(800,400))
plot_cluster_results!(fig, centers, data_labels, data_2, samples_2)
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220

GMM

# For dataset 1
Random.seed!(2)
k = 5
means = kpp_init(data_1, k)
vars = []
for i in 1:k
    A = I(2) .+ rand(2,2)
    push!(vars,A' * A)
end
gaussians = [MvNormal(means[:,i],vars[i]) for i in 1:k]
data_labels = ones(size(data_2,2))

gmm!!(gaussians, data_labels, data_1)

fig = Figure(size=(800,400))
plot_gmm_results!(fig, gaussians, data_labels, data_1, samples_1)
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220

# For dataset 2
Random.seed!(2)
k = 5
means = kpp_init(data_2, k)
vars = []
for i in 1:k
    A = I(2) .+ rand(2,2)
    push!(vars,A' * A)
end
gaussians = [MvNormal(means[:,i],vars[i]) for i in 1:k]
data_labels = ones(size(data_2,2))

gmm!!(gaussians, data_labels, data_2)

fig = Figure(size=(800,400))
plot_gmm_results!(fig, gaussians, data_labels, data_2, samples_2)
┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions.
└ @ Makie ~/.julia/packages/Makie/VRavR/src/scenes.jl:220

Great fits!